Count by 653 (Skip Counting by 653s)

Count by 653

Here we will show you how to count by 653, discuss counting by 653 patterns, and tell you why knowing how to count by 653 matters. To start off, note that Count by 653 means counting in 653s, or count by six hundred fifty-threes, and it is also called skip counting by 653.

How to count by 653
Normally, we would count by 1 like this: 1, 2, 3, 4, etc., but when we count by 653, we count 653, 1306, 1959, 2612, and so on.

In other words, to count in intervals of 653 or skip counting by 653, we start with 653 and then add 653 to get the next number, and then continue adding 653 to the previous number to keep counting by 653, like this:

653
653 + 653 = 1306
1306 + 653 = 1959
1959 + 653 = 2612
2612 + 653 = 3265
...

You can of course skip count by 653 forever, so it is impossible to make a list of all numbers, but below is a Count by 653 Chart of the first 100 numbers to get you started.

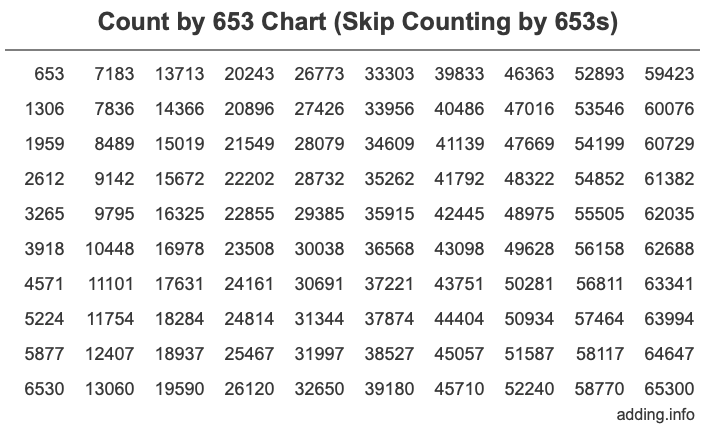
Looking at the chart above, you will see that the first column has the first ten numbers you get when you skip count by 653, the second column has the next ten numbers you get when you skip count by 653, and so forth.

Count by 653 Patterns
We organized the Skip Counting by 653s Chart above in 10 rows and 10 columns so you can easily identify patterns.

Skip counting always creates patterns. Figuring out these patterns may help you if want to count by 653, but don't have the Counting by 653s Chart above. Obviously, one pattern with counting by 653s is that the number increases by 653.

Furthermore, if you look at each row above, each number in the row has the same last digit (ones place). That means that every tenth number has the same last digit.

If you look down the columns, you will see that the last digit (ones place) repeats itself in blocks of 10 over and over. The pattern of the last digit when you count by 653 goes 3, 6, 9, 2, 5, 8, 1, 4, 7, 0 and 3, 6, 9, 2, 5, 8, 1, 4, 7, 0 and so on for as long as you count by 653.

Why Count by 653?
We think that understanding and learning about skip counting by 653 is important, because it teaches you how the arithmetic operations fit together. Below are some examples of what we mean.

When you count by six hundred fifty-three, you are also creating a list of multiples of 653 that you can use in math when you need the least common multiple. 653 times n equals the nth multiple or skip count of 653.

When you skip count by 653, you are also creating a list of numbers that 653 is divisible by. On top of that, skip counting by 653 is the same as making the 653 times table.

Skip Counting
Need to skip count by another number? Enter another number for us to skip count for you.

Count by 654
Here is the next number on our list that we used to skip count.