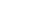To find the answer to "What two numbers have a product of 42 and a sum of 153?" we first state what we know. We are looking for x and y and we know that x • y = 42 and x + y = 153.
Before we keep going, it is important to know that x • y is the same as y • x and x + y is the same as y + x. The two variables are interchangeable. Which means that when we create one equation to solve the problem, we will have two answers.
To solve the problem, we take x + y = 153 and solve it for y to get y = 153 - x. Then, we replace y in x • y = 42 with 153 - x to get this:
x • (153 - x) = 42
Like we said above, the x and y are interchangeable, therefore the x in the equation above could also be y. The bottom line is that when we solved the equation we got two answers which are the two numbers that have a product of 42 and a sum of 153. The numbers are:
0.275
152.725
That's it! The two numbers that have a product of 42 and a sum of 153 are 0.275 and 152.725 as proven below:
0.275 • 152.725 ≈ 42
0.275 + 152.725 = 153
Note: Answers are rounded up to the nearest five decimals if necessary so the answers may not be exact.
Product Sum Calculator
Need the answer to a similar problem? Submit another product and sum below to find the two numbers that make your product and sum.